Heterogeneidad: ¿qué es y por qué es importante?
Publicado el mayo 12, 2022 por Maximilian Siebert
Traductora: Pamela Villacorta Landeo – ADIECS (Asociación para el Desarrollo de la Investigación Estudiantil en Ciencias de la Salud)
La heterogeneidad no es algo que deba temerse, solo significa que hay variabilidad en tus datos. Por lo que, si se reúnen diferentes estudios para analizarlos o hacer meta-análisis, está claro que se encontrarán diferencias. Lo opuesto a la heterogeneidad es la homogeneidad, que significa que todos los estudios muestran el mismo efecto.
Es importante señalar que existen diferentes tipos de heterogeneidad:
- Clínica: diferencia en los participantes, las intervenciones o los resultados.
- Metodológica: diferencias en los diseños de estudio, riesgo de sesgo.
- Estadística: variación en los efectos o resultados de la intervención.
Nos interesan estas diferencias porque pueden indicar que nuestra intervención puede no estar funcionando de la misma manera cada vez que se utiliza. Al investigar estas diferencias, se puede llegar a una mayor comprensión de los factores que influyen en la intervención, y del resultado que se puede esperar la próxima vez que se aplique la intervención.
Aunque la heterogeneidad clínica y metodológica son importantes, este blog se centrará en la heterogeneidad estadística.
Cómo identificar y medir la heterogeneidad
Prueba visual (Eyeball test)
En su diagrama de bosque, fíjese en los intervalos de confianza superpuestos, en vez del lado en el que se encuentran las estimaciones del efecto. El hecho de que los resultados estén a ambos lados de la línea de no efecto, puede no afectar su evaluación de la presencia de heterogeneidad, pero puede influir en su evaluación de si la heterogeneidad es importante.
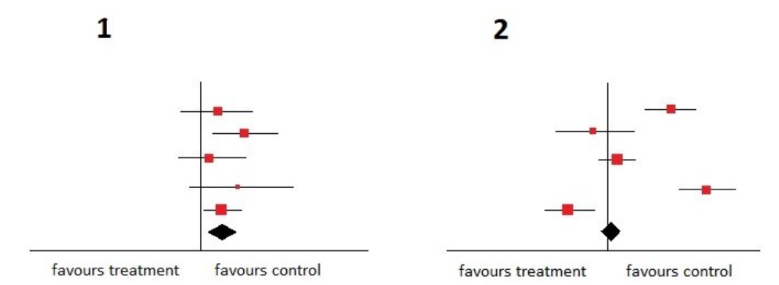
Por supuesto, el más homogéneo es el diagrama número 1. Los intervalos de confianza se superponen y, además, todos los estudios se encuentran a favor del control.
Para las personas a las que les gusta medir las cosas en lugar de solo mirarlas, no se preocupen, todavía hay algunos métodos estadísticos que les ayudarán a captar el concepto de heterogeneidad.
Test de Chi-cuadrado (χ²) (Chi-squared test)
Esta prueba asume la hipótesis nula de que todos los estudios son homogéneos, o de que cada estudio está midiendo un efecto idéntico, y nos da valor p para probar esta hipótesis. Si el valor p de la prueba es bajo, se puede rechazar la hipótesis y la heterogeneidad estaría presente.
Como la prueba no suele ser lo suficientemente sensible y puede suceder rápidamente la exclusión equivocada de la heterogeneidad, muchos científicos utilizan un valor p de ≤ 0.1 en lugar de ≤ 0.05 como punto de corte.
I^2
Esta prueba fue desarrollada por el profesor Julian Higgins, y tiene una teoría para medir el grado de heterogeneidad en lugar de afirmar si está presente o no.
Los umbrales para la interpretación de I² pueden ser engañosos, ya que la importancia de la inconsistencia depende de varios factores. Una guía aproximada de interpretación es la siguiente:
- 0% al 40%: podría ser no importante
- 30% al 60%: heterogeneidad moderada
- 50% al 90%: heterogeneidad sustancial
- 75% al 100%: heterogeneidad considerable
Para entender la teoría anterior, mire el siguiente ejemplo:
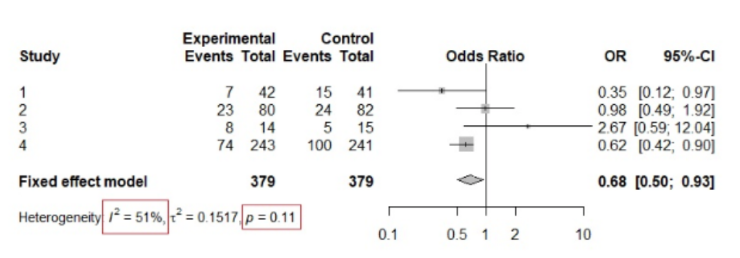
Podemos ver que el p-valor de la prueba de chi-cuadrado es 0,11, confirmando la hipótesis nula y sugiriendo homogeneidad. Sin embargo, al observar las intervenciones podemos ver cierta heterogeneidad en los resultados. Es más, el valor I² es del 51%, lo que sugiere una heterogeneidad entre moderada y sustancial.
Este es un buen ejemplo de cómo la prueba de χ² puede ser engañosa cuando hay pocos estudios en el meta-análisis.
¿Cómo manejar la heterogeneidad?
Una vez que haya detectado la variabilidad en sus resultados, debe tratarla. Estos son algunos pasos para tratar este problema:
- Compruebe sus datos para ver si hay errores – Vuelva atrás y vea si ha escrito algo mal.
- No haga un meta-análisis si la heterogeneidad es demasiado alta – No todas las revisiones sistemáticas necesitan un meta-análisis.
- Explore la heterogeneidad – Esto puede hacerse mediante un análisis de subgrupos o una meta-regresión.
- Realice un meta-análisis de efectos aleatorios – Tenga en cuenta que este enfoque es para la heterogeneidad que no se puede explicar porque se debe al azar.
- Cambie las medidas de efecto – Digamos que se utiliza la diferencia de riesgo y se tiene una alta heterogeneidad, entonces pruebe con riesgo relativo u odds ratio.
Autor y Link original: Maximilian Siebert – «What is heterogeneity?»
Bibliografía
[1] Fletcher, J. What is heterogeneity and is it important? BMJ 2007; 334 :94. [Internet] [Consultado el 03 de marzo del 2022] Disponible en: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1767262/
*Nota de traductor: el enlace citado en el artículo original de esta traducción cuenta con una corrección. Puedes encontrar la corrección en la siguiente cita: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1796735/
[2] Deeks JJ, Higgins JPT, Altman DG (editors). Chapter 9: Analysing data and undertaking meta-analyses. In: Higgins JPT, Green S (editors). Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 [updated March 2011]. The Cochrane Collaboration, 2011. [Internet] [Consultado el 03 de marzo del 2022] Disponible en: https://handbook-5-1.cochrane.org
*Nota de traductor: el enlace citado en el artículo original de esta traducción cuenta con una actualización. Puedes encontrar la versión 6.3, 2022: https://training.cochrane.org/handbook/current
[3] Math is Fun. Chi square test. [Internet] [Consultado el 03 de marzo del 2022] Disponible en: https://www.mathsisfun.com/data/chi-square-test.html
