Ensayos aleatorizados por conglomerados: conceptos

Publicado el julio 11, 2023 por Vinay Jaikumar

Traductor:  Ana María Rojas-Gómez – Epistemonikos / Cochrane US Mentee (Y2)

Autor y Artículo original: Vinay Jaikumar – «Cluster Randomized Trials: Concepts» 

¿Qué es la aleatorización por conglomerados?

En la mayoría de los ensayos clínicos, los participantes son asignados aleatoriamente a los diferentes grupos de tratamiento de forma individual. Sin embargo, en circunstancias en las que no se puede llevar a cabo la asignación aleatoria individual (por ejemplo, debido a desafíos prácticos) o no es deseable (por ejemplo, debido a la contaminación), los participantes son asignados aleatoriamente como «grupos de individuos» o conglomerados (Figura 1 ). En la aleatorización por conglomerados, los grupos de participantes, como servicios hospitalarios, escuelas, unidades de hospital/UCI o áreas geográficas/regionales, sirven como unidad de asignación aleatoria. La aleatorización por conglomerados es particularmente adecuada para estudios de implementación, como intervenciones de estilo de vida en la población, resultados de las directrices de tratamiento y vacunaciones comunitarias(1–3).

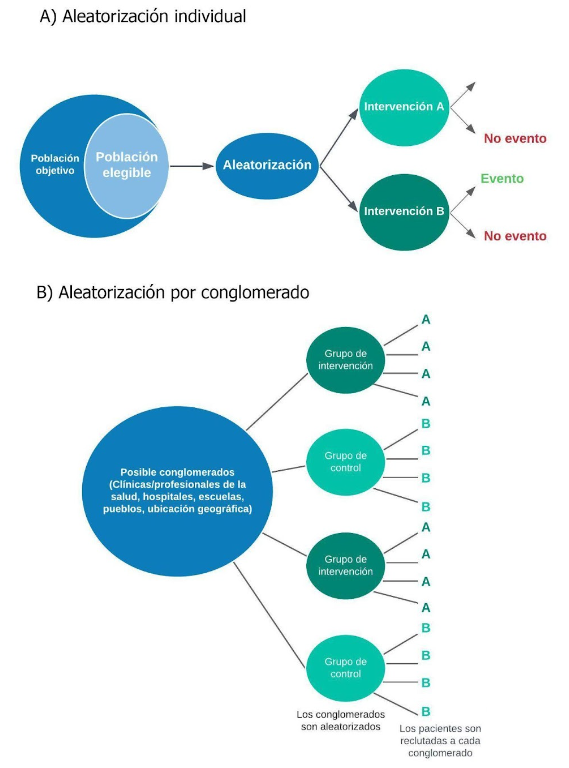
Figura 1

https://ibb.co/tJG1657

¿Por qué deberíamos considerar la aleatorización por conglomerados? 

• Viabilidad práctica de la aleatorización por conglomerados

Algunas intervenciones pueden ser factibles sólo mediante el enfoque de aleatorización por grupos (1–3). Por ejemplo, consideremos el Estudio sobre Sustitución de Sal y Accidentes Cerebrovasculares (SSaSS) realizado en localidades chinas. En este ensayo aleatorizado por conglomerados, abierto y a gran escala, participaron 600 aldeas de China con 21,000 participantes  (35 participantes por localidad) (4). Los participantes tenían antecedentes de ictus, ≥60 años o padecían hipertensión arterial. Se estudió el impacto de la sustitución de la sal (75% : 25% = cloruro de sodio : cloruro de potasio frente a sólo cloruro de sodio) en posteriores accidentes cerebrovasculares, eventos cardiovasculares y muerte. El diseño de los ensayos agrupados requiere un tamaño de muestra tan elevado. Si tuviéramos que considerar la aleatorización individual dentro de cada localidad, habría que contemplar los requisitos logísticos de implementar los procedimientos de consentimiento, la aleatorización y ambas intervenciones de tratamiento en cada una de las 600 localidades. Sería más factible y eficiente que cada localidad/grupo se asignara aleatoriamente a la intervención y al control.

• Contaminación en la aleatorización por conglomerados

La contaminación es un escenario en el que el grupo de control recibe la intervención por parte de los participantes del grupo de intervención o por otros medios (2,3,5). Esto tiende a diluir el efecto de la intervención en comparación con los controles, lo que lleva a un error de Tipo II.

Por ejemplo, consideremos un ensayo de vacunas en una población para una enfermedad transmisible en la que la vacuna es capaz de inducir la inmunidad colectiva. Si los participantes se asignan al azar de manera individual, debido al efecto colectivo, los controles demostrarán una resistencia aumentada a la enfermedad comparable al grupo de intervención. Esto subestima o diluye el impacto beneficioso que la vacuna proporciona sobre el grupo de control (Figura 2A). Aquí, utilizamos un enfoque de aleatorización por conglomerados. Si agrupamos a los participantes regionalmente/de acuerdo con su localidad y los asignamos al azar a dos profesionales clínicos, uno designado para administrar la vacuna y otro como control, la posibilidad de que se produzca la inmunidad colectiva se reducirá (Figura 2B)

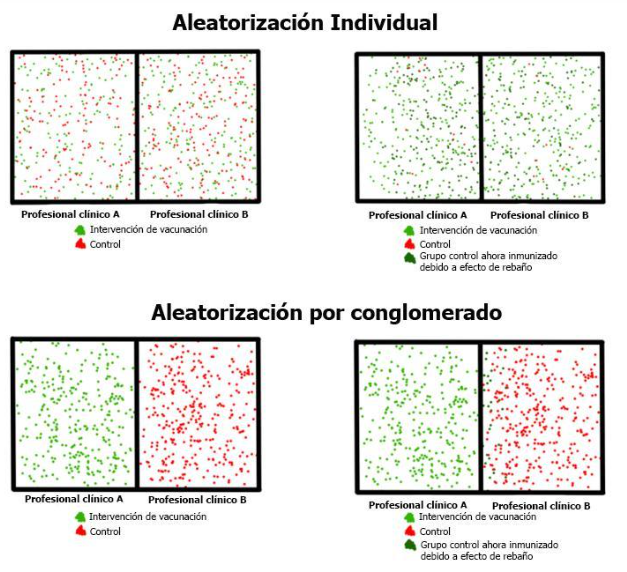
Figura 2

https://ibb.co/dpnH9Fd

De manera similar, los ensayos que utilizan una intervención educativa para mejorar el estilo de vida de los participantes con alto riesgo de una enfermedad podrían aleatorizar a los participantes en grupos para evitar una mayor posibilidad de que el grupo de intervención informe al grupo de control sobre el tratamiento. Un aumento en el porcentaje de contaminación disminuye la potencia del estudio y requiere un aumento en el tamaño de la muestra para mantener la potencia (Figura 3) (2).

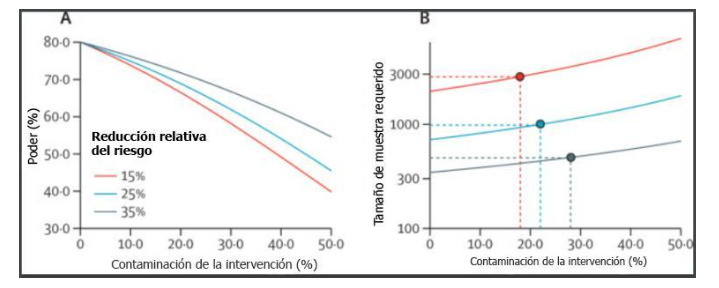
Figura 3- Dron et al (2)

https://ibb.co/fd693Rx

Sin embargo, aunque la agrupación puede mitigar el impacto de la contaminación, no está completamente a salvo de ella. Grandes cantidades de contaminación pueden superar la capacidad de agrupamiento para mitigarlas. Por ejemplo, consideremos el ensayo IMPACT-AF (6). Exploraron el papel de los programas educativos continuos y el monitoreo y la retroalimentación regulares para promover la adherencia a los anticoagulantes entre dos grupos de poblaciones aleatorias con fibrilación auricular.

El primer grupo  ya había recibido una intervención educativa inicial de centros de tratamiento experimentados y el segundo grupo no.  El segundo grupo, que no había recibido educación inicial, mostró una mayor proporción de grupos que se adhirieron al anticoagulante en el seguimiento de 6 y 12 meses después de la intervención y el control no. Sin embargo, el primer grupo mostró tasas similares de adherencia entre los grupos de intervención y control en el seguimiento de 6 y 12 meses. Esto es explicable considerando que el brazo de control del primer grupo recibió la misma intervención educativa o contaminación inicialmente de la institución experimentada

Esto constituye una explicación plausible para no observar una pérdida de adherencia tras la ausencia de educación continua en el grupo de control del primer grupo. Esto diluyó o subestimó el impacto de las intervenciones educativas en la mejora/mantenimiento de las tasas de cumplimiento entre los grupos de intervención y control. Sin embargo, leyendo entre líneas, este estudio transmitió que las intervenciones educativas iniciales serán suficientes para mantener excelentes tasas de adherencia al tratamiento, incluso en ausencia de una intervención educativa continua (6).

• Consentimiento en la aleatorización por conglomerados

En los ensayos que emplean la aleatorización individual, el consentimiento suele preceder al proceso de aleatorización (1,2). En los ensayos por conglomerados, los conglomerados se aleatorizan inicialmente y se designan como brazo de intervención o control, después de lo cual se asigna a los participantes a cada brazo. El consentimiento individual a menudo puede ser dispensado en los ensayos por conglomerados (1,2). En tales escenarios, solo se requiere el consentimiento del representante del conglomerado (médico, hospital, director de escuela, jefe de la aldea). Sin embargo, cuando las circunstancias requieren el proceso de consentimiento informado, entra en juego una consideración importante. Se ha observado cierta negativa al tratamiento o recopilación de datos en ensayos con aleatorización individual cuando el consentimiento se adquiere después del proceso de aleatorización en lugar de precederlo (3,7,8). Esto también introducirá un sesgo de selección en los ensayos por conglomerados. Identificar e informar a todos los participantes potenciales dentro de los conglomerados sobre todas las posibles alternativas de intervención, seguido de solicitar su consentimiento para participar, puede superar este obstáculo.

Desafíos asociados con los ensayos aleatorizados por conglomerado

• Calculando el tamaño de la muestra

En comparación con los ensayos que emplean la aleatorización individual para probar una hipótesis, los ensayos de aleatorización por conglomerados requieren un tamaño de muestra significativamente mayor para probar lo mismo. Esto se debe a que las mediciones de resultados de los participantes dentro de un conglomerado tienden a ser más similares en comparación con las de otros conglomerados. Esto indica que esas observaciones no son independientes y que están correlacionadas en una aleatorización por conglomerados en comparación con la aleatorización individual, donde se asume que las observaciones no están correlacionadas durante el cálculo del tamaño de muestra. La varianza mide la correlación entre los resultados. Representa cuán alejadas están las observaciones de la media. La varianza nunca puede ser negativa. Una varianza de cero implica que todas las observaciones son iguales y no hay dispersión en ninguno de los lados de la media.

La estimación del tamaño de muestra para la aleatorización por conglomerados debe considerar la varianza dentro de los conglomerados (σw2) así como la varianza entre diferentes conglomerados (σb2). El Coeficiente de Correlación Intraclase (ICC, por sus siglas en inglés) cuantifica la proporción de la varianza total (σw2 + σb2) de la variable de resultado que se explica por la varianza entre conglomerados (σb2) y se designa con el símbolo rho (ρ) (1,2). Las varianzas se derivan de estudios previos. También se debe tener en cuenta que se utilizan variaciones del ICC para cuantificar la concordancia entre evaluadores donde se comparan los valores medidos/registrados para ver si son análogos entre los evaluadores

ICC (ρ) = σb2 / σw2 + σb2

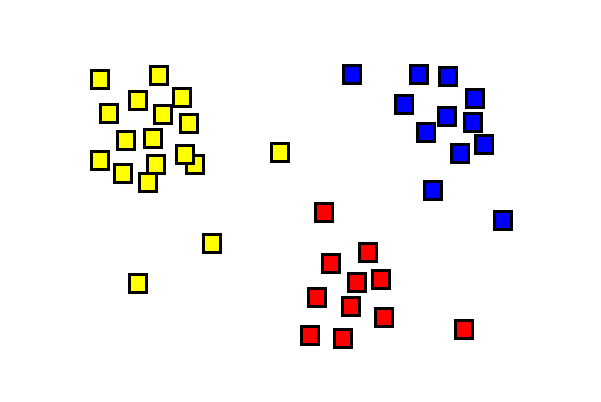
Si σw2 es cero, es decir, los resultados dentro de un conglomerado son los mismos con poca o ninguna variación, entonces ρ es uno (Figura 4B). En consecuencia, si σb2 es cero, es decir, el resultado entre conglomerados es el mismo con poca o ninguna variación, entonces ρ también es cero (Figura 4A).

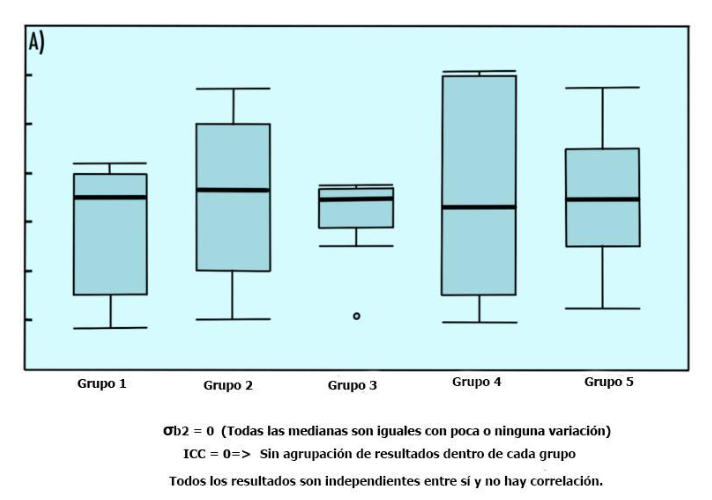
Figura 4A

https://ibb.co/NF1CZwy

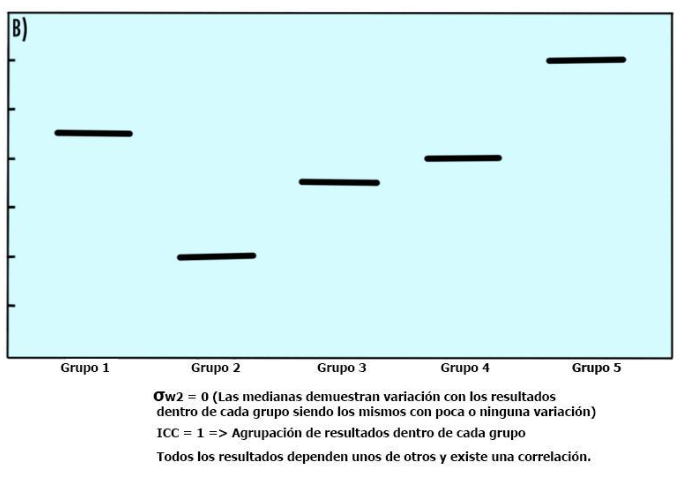
 Figura 4B

https://ibb.co/9V9FjMg

El ρ encuentra utilidad en el cálculo del efecto de diseño. Esto representa el factor de inflación por el cual se debe aumentar el tamaño de la muestra para mantener el poder del ensayo aleatorizado por conglomerados (1,2). El efecto de diseño se calcula por:

deff = 1 + (m – 1) ρ

Donde m es el tamaño del conglomerado y ρ es el coeficiente de correlación intraclase. Ahora, el tamaño de muestra total (N) necesario para llevar a cabo un ensayo aleatorizado por conglomerados es:

N = n (deff)  or  N = n (1 + (m – 1) ρ)

donde n es el tamaño de muestra requerido si se realizara una aleatorización individual. N es el tamaño total de muestra que requiere una inflación de deff veces n (1,2). Si el tamaño de cluster es 1 (m=1) o ρ es cero (no hay variación entre clusters/los clusters son iguales/σb2 es cero), deff es 1 y el tamaño de muestra para el ensayo con aleatorización de cluster es igual al de un ensayo con aleatorización individual. Si ρ es uno (no hay variación dentro de un cluster/las observaciones dentro de un cluster son iguales/σw2 es cero), el tamaño de muestra requerido para el ensayo con aleatorización de cluster se multiplica por un factor ρ. Por lo tanto, si se observa una mayor correlación entre los participantes dentro de un cluster, se obtiene un ρ mayor. Esto conduce a un tamaño de muestra más grande que ahora será suficiente para estimaciones de efecto precisas (1,2).

Cuanto mayor sea el valor de ρ, mayor será el tamaño de muestra necesario, y la diferencia puede ser significativa. Consideremos un m de 30. El aumento en el tamaño de muestra para valores crecientes de ρ de 0,001, 0,01 y 0,1 será por un factor de 1,029, 1,249 y 3,49 respectivamente.

•  Efectos de agrupamiento:

En un entorno con agrupaciones, los resultados de los participantes tienden a estar correlacionados, lo que puede atribuirse a un factor común. En términos más simples, los participantes dentro de una agrupación tenderán a tener resultados similares. Por ejemplo, los factores del paciente, como la edad, la etnia, el género, la ubicación geográfica o los planes de seguros, pueden influir en su reclutamiento bajo ciertos médicos y hospitales. Los atributos a nivel de agrupación, como las tasas de cumplimiento de los médicos con las decisiones clínicas establecidas para el ensayo, asegurarán que todos los participantes bajo ese médico reciban exactamente el mismo tratamiento. Por lo tanto, los participantes dentro de una agrupación mostrarán resultados más similares en comparación con otras agrupaciones. Además, los participantes dentro de una agrupación pueden influirse mutuamente a través de actitudes y comportamientos similares, lo que resulta en tasas similares de cumplimiento con el tratamiento o el seguimiento, y resultados. El agrupamiento no solo afecta a los ensayos de agrupación, sino también a los ensayos con asignación individual aleatoria (1,2,9).

Consideremos un estudio de aleatorización individual donde se eligen diferentes centros (por ejemplo, geográficamente separados) (Figura 6). Los participantes de cada centro incluirán tanto participantes de intervención como de control. Los participantes dentro de cada centro tenderán a mostrar resultados similares con poca o ninguna variabilidad (Figura 6, curvas rojas) en comparación con los participantes de un centro diferente. Ahora, combinamos todos los resultados de los participantes de intervención en todos los centros y compararlos con los resultados de los participantes de control agrupados. Si no se tiene en cuenta el efecto del agrupamiento, aunque la variación en los resultados puede ser pequeña dentro de cada centro, será relativamente mucho mayor entre los centros, lo que dará lugar a desviaciones estándar innecesariamente grandes, valores p mayores, intervalos de confianza más amplios y resultados falsos negativos (Figura 5A). Considerar el efecto del agrupamiento mitiga esa correlación de resultados y da como resultado estimaciones precisas de los resultados (Figura 5B) (1,2,9).

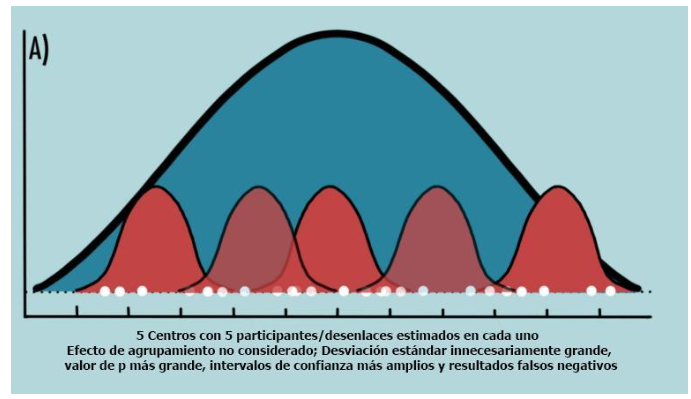
Figura 5A

https://ibb.co/fMdjSf8

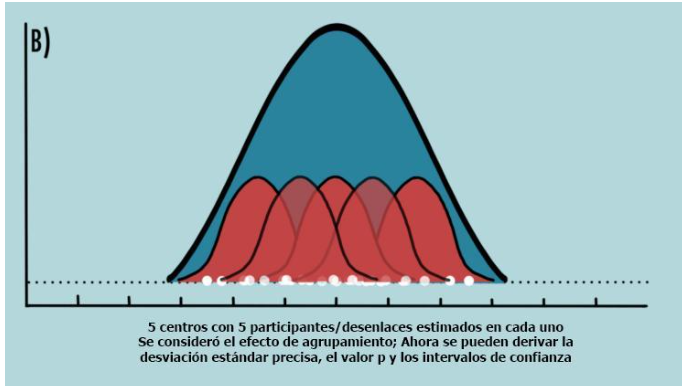
Figura 5B

https://ibb.co/gVpQCB0

En los ensayos grupales, este efecto se amplifica ya que los grupos tienen participantes de intervención o participantes de control, pero no ambos. Si los resultados del grupo de intervención muestran una fuerte correlación positiva/negativa, si no se considera el impacto del agrupamiento, esto puede incluso conducir a resultados falsos positivos o falsos negativos, respectivamente, con valores de p inapropiadamente pequeños e intervalos de confianza estrechos. El análisis que considera los efectos de agrupamiento calculará con precisión la varianza de las estimaciones de resultados (1,2,9).

• Sesgo de selección: 

El sesgo de selección en los ensayos de conglomerados puede ser introducido tanto a nivel de conglomerado como a nivel de participante (1–3,9). La aleatorización inicial de los conglomerados es un paso crucial y propenso a una asignación sesgada. Si los conglomerados se asignan en función de los resultados predecibles de la población de participantes aún no reclutados, esto introduce un sesgo de selección(1–3,9). A nivel individual, si un participante tiene características que predicen un resultado independientemente de la intervención o el control, se puede colocar selectivamente al participante en cualquiera de los conglomerados dependiendo de qué resultado se quiera observar. Por ejemplo, si se sabe que un participante reclutado muestra un resultado desfavorable, puede ser reclutado en el grupo de control o se le puede negar la participación en el grupo de intervención(1–3,9).

• Calidad del ensayo:

Mantener la calidad general de seguir el protocolo del ensayo y la calidad / seguimiento de los datos es una consideración importante en un ensayo de conglomerados logísticamente desafiante (2).

Bibliografía:

1. Design and Analysis of Cluster Randomization Trials in Health Research | Wiley [Internet]. Wiley.com. [citado 27 de abril de 2023]. Disponible en: https://www.wiley.com/en-us/Design+and+Analysis+of+Cluster+Randomization+Trials+in+Health+Research-p-9780470711002
2. Dron L, Taljaard M, Cheung YB, Grais R, Ford N, Thorlund K, et al. The role and challenges of cluster randomised trials for global health. Lancet Glob Health. mayo de 2021;9(5):e701-10.
3. S P, Dj T, J W. Cluster randomized controlled trials. J Eval Clin Pract [Internet]. octubre de 2005 [citado 27 de abril de 2023];11(5). Disponible en: https://pubmed.ncbi.nlm.nih.gov/16164589/
4. Effect of Salt Substitution on Cardiovascular Events and Death | NEJM [Internet]. [citado 27 de abril de 2023]. Disponible en: https://www.nejm.org/doi/10.1056/NEJMoa2105675
5. Slymen DJ, Hovell MF. Cluster versus individual randomization in adolescent tobacco and alcohol studies: illustrations for design decisions. Int J Epidemiol. 1 de agosto de 1997;26(4):765-71.
6. Vinereanu D, Lopes RD, Bahit MC, Xavier D, Jiang J, Al-Khalidi HR, et al. A multifaceted intervention to improve treatment with oral anticoagulants in atrial fibrillation (IMPACT-AF): an international, cluster-randomised trial. Lancet Lond Engl. 14 de octubre de 2017;390(10104):1737-46.
7. Zelen M. Randomized consent designs for clinical trials: An update. Stat Med. 1990;9(6):645-56.
8. Altman DG, Whitehead J, Parmar MKB, Stenning SP, Fayers PM, Machin D. Randomised consent designs in cancer clinical trials. Eur J Cancer. 1 de noviembre de 1995;31(12):1934-44.
9. Chuang JH, Hripcsak G, Heitjan DF. Design and Analysis of Controlled Trials in Naturally Clustered Environments: Implications for Medical Informatics. J Am Med Inform Assoc. 1 de mayo de 2002;9(3):230-8.

Tags: